I'm sad to say that this is the end of my posting here. I have finished my Masters and will be graduating on Friday with a First Class Honours in Engineering Mathematics. Whoop! I don't think I could have done it in quite as much style if I hadn't had this blog to blow off some steam and help my thought processes out.
It may be the end of this blog but as I go out into the wide world of possibilities I do think that perhaps one day I will do a PhD and then a blog of similar form shall emerge to keep me going through that. So one day we will be reunited in the struggle to understand a bit more about the world around us in a wonderfully engineering mathematical way!
Thanks for watching!
If you would like to make contact in the future please use: bp3TT.7@gmail.com (the email for me here) or comment on a post and I will get back to you.
Maddy's Masters Madness
Tuesday 12 July 2011
Monday 2 May 2011
Finish line
Here we are. I'm done. My thesis is written. My poster is printed. My webpage is uploaded and ready for viewing. And all one day before the deadline too! This makes today notable not just for Osama Bin Laden's death. :)
It has been a slog as I am sure you could tell. I managed to plough some understanding out of the murky subject of two-dimensional noninvertible maps. And now I pass it to you.
My webpage is available for your viewing pleasure.
On it are links to my poster and thesis. (Ah, just tried to upload my thesis pdf to it and it didn't work...I'll try again tomorrow so check for it then!).
*dusts hands off* Right that's a third of this year and 16.667% of my degree done. Onwards to viva and exams!
It has been a slog as I am sure you could tell. I managed to plough some understanding out of the murky subject of two-dimensional noninvertible maps. And now I pass it to you.
My webpage is available for your viewing pleasure.
On it are links to my poster and thesis. (Ah, just tried to upload my thesis pdf to it and it didn't work...I'll try again tomorrow so check for it then!).
*dusts hands off* Right that's a third of this year and 16.667% of my degree done. Onwards to viva and exams!
Wednesday 27 April 2011
Poster!
So, long time, no post. However these last couple weeks have been crucial for my thesis and all the extras and the next week is not going to be fun either since I hand in everything on Tuesday. *sarcastic yay!*
However, I did say I would put up my poster. Enjoy. Let me know how cool you think it is on a scale from -10 to 10. :-)
Soon I will link this to the website I am producing for the project so you have the complete picture of my year's work.
However, I did say I would put up my poster. Enjoy. Let me know how cool you think it is on a scale from -10 to 10. :-)
Soon I will link this to the website I am producing for the project so you have the complete picture of my year's work.
Friday 8 April 2011
On a less serious note
So, I realised just a few minutes ago that I haven't written about chaotic attractors in all their splendour. An incredible oversight on my part. These objects are achingly beautiful and intricately complex in form. They arise in phase space (I believe I have covered this) in certain parameter regions of systems. Their fractal geometry means that dynamics is incredibly sensitive on them and while trajectories will follow the path of the attractor (duh! attracting :-) ), there is no predicting which exact part of the attractor it will land on and follow round or ultimately where it will end up. The attractor is fixed, the trajectories are not. A nice succinct explanation is available here.
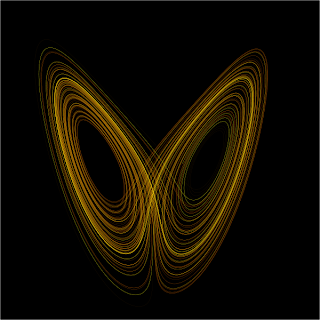
The one that ties in closest to my work is the Lorenz attractor. The three dimensional system for describing turbulence gives birth to an amazing structure. This attractor is where the 'butterfly effect' expression originated. The attractor itself is geometrically between two and three dimensions and winds itself around two points.
The image (from wiki) shows exactly this. Where the trajectories 'cross' in this two-dimensional visualisation is actually where they layer over each other - manifolds cannot intersect (the unstable manifold exactly describes the attractor). The view is better in 3d. The fractal (Hausdorff) dimension of the attractor is about 2.06.
Other systems with strange attractors are the Rossler system and Henon map. This page gives a nice description and a few images.
As a side note: for those of you who read and enjoyed 'Harry Potter and the Methods of Rationality' or 'Luminosity' I would recommend this strangely named (but you'll understand all too soon) 'Baby Eating Aliens' also from the Less Wrong family and the (there is a theme here, no?) 'Harry Potter and the Wastelands of Time' if you like a bit of complex, epic writing with lots of action and magic!
Enjoy! Also, something to look forward to: I hope to have my poster available for you lot next time I post. :D
Doh! Almost forgot. One of the lecturers at my university (Hinke Osinga) actually crocheted the Lorenz stable manifold! If you want to know how, read this!
Incidentally, my project supervisor is the Bernd Krauskopf mentioned in the article. And yes, it is one of their Christmas decorations. ;)
The one that ties in closest to my work is the Lorenz attractor. The three dimensional system for describing turbulence gives birth to an amazing structure. This attractor is where the 'butterfly effect' expression originated. The attractor itself is geometrically between two and three dimensions and winds itself around two points.
The image (from wiki) shows exactly this. Where the trajectories 'cross' in this two-dimensional visualisation is actually where they layer over each other - manifolds cannot intersect (the unstable manifold exactly describes the attractor). The view is better in 3d. The fractal (Hausdorff) dimension of the attractor is about 2.06.
Other systems with strange attractors are the Rossler system and Henon map. This page gives a nice description and a few images.
As a side note: for those of you who read and enjoyed 'Harry Potter and the Methods of Rationality' or 'Luminosity' I would recommend this strangely named (but you'll understand all too soon) 'Baby Eating Aliens' also from the Less Wrong family and the (there is a theme here, no?) 'Harry Potter and the Wastelands of Time' if you like a bit of complex, epic writing with lots of action and magic!
Enjoy! Also, something to look forward to: I hope to have my poster available for you lot next time I post. :D
Doh! Almost forgot. One of the lecturers at my university (Hinke Osinga) actually crocheted the Lorenz stable manifold! If you want to know how, read this!
Incidentally, my project supervisor is the Bernd Krauskopf mentioned in the article. And yes, it is one of their Christmas decorations. ;)
Wednesday 30 March 2011
Horseshoe Chaos
While I struggle with supposedly impossible inversions, I'd like to introduce you all to Smale's horseshoe. This object is where the definition of chaos originates yet it is a relatively simple idea.
You start with a square. Squish is down and pull it out to the sides then bend it at the halfway point so it looks like a horseshoe. Then replace it over the square so that the two lengths form vertical strips on the square. This is the basic transformation of the horseshoe map. It is also invertible. Take the bent strips, rotate back to horizontal, and unbend it then squish it in from the sides and pull from the top and bottom then you get the square again. If you do this inversion again you get strips intersection horizontally.
Repeatedly performing the forward transformations you get more and increasingly thin vertical strips: 2 strips become 4, 4 strips become 8 i.e. each strip gets two thinner strips within it at each iteration. Doing the same backwards, you get lots of increasingly thinner horizontal strips. The points in the strips are the points that remain in the set at that iteration. Most points leave after even just a few iterations in either direction.
If you overlay the two directions, the points at the intersections that remain in the square under all iterations (if you iterate infinitely in either direction). This is the invariant set. This set is a Cantor set (disconnected and unstable fractal).
If you labelled each point with 0 or 1 at each iteration you could describe the positions of all the points in the square e.g. .0101 means a point that is in the 6th vertical strip after four iterations (the right hand strip of the left hand strip of the right hand strip of the left hand strip in the first iteration) or
If you can see that...sorry if it's too small.
Since you can do this in both directions, the whole dynamics of any point in the square can be described by it's bi-infinite sequence of positions.
Knowing this we can construct any orbit we like and we know it will describe at least one point in the square.
So we can make a periodic point: ...010101.0101010... which alternates from the left to the right. Since we have infinite lengths in both direction, we can make (uncountably) infinitely many of these periodic points.
Or we can make a non-periodic point: ...010001101100000.1010100110111... by, for example, 'counting' in binary as above or just by adding the wrong value to a periodic point i.e. ...01010101.0101011...is non-periodic. There are (uncountably) infinite of these too.
Among this set of non-periodic orbits we can find at least one that comes arbitrarily close to the invariant set. This is trivial since you can take just part of the sequence that describes a point in the invariant set and it would come as close as you like!
I hope you are following since I have just demonstrated that Smale's horseshoe perfectly defines chaos.
Chaotic motion must consist of the following:
- infinitely many periodic orbits
- non-periodic orbits
- dense orbits - ones that come arbitrarily close to any point in the set.
There tends also to be the condition of sensitive dependence on initial conditions but this can be shown through the dense orbits - you can take two sequences that are the same for any arbitrary iterations and in the next they can end up in two different strips i.e. they may start very close but can end up very far apart.
Voila!
Strogatz does give a very basic introduction but for a more detailed approach read the first chapter of "Elements of Applied Bifurcation Theory" by Yuri Kuznetsov. Wiki also has its own explanation.
You start with a square. Squish is down and pull it out to the sides then bend it at the halfway point so it looks like a horseshoe. Then replace it over the square so that the two lengths form vertical strips on the square. This is the basic transformation of the horseshoe map. It is also invertible. Take the bent strips, rotate back to horizontal, and unbend it then squish it in from the sides and pull from the top and bottom then you get the square again. If you do this inversion again you get strips intersection horizontally.
Repeatedly performing the forward transformations you get more and increasingly thin vertical strips: 2 strips become 4, 4 strips become 8 i.e. each strip gets two thinner strips within it at each iteration. Doing the same backwards, you get lots of increasingly thinner horizontal strips. The points in the strips are the points that remain in the set at that iteration. Most points leave after even just a few iterations in either direction.
If you overlay the two directions, the points at the intersections that remain in the square under all iterations (if you iterate infinitely in either direction). This is the invariant set. This set is a Cantor set (disconnected and unstable fractal).
If you labelled each point with 0 or 1 at each iteration you could describe the positions of all the points in the square e.g. .0101 means a point that is in the 6th vertical strip after four iterations (the right hand strip of the left hand strip of the right hand strip of the left hand strip in the first iteration) or
If you can see that...sorry if it's too small.
Since you can do this in both directions, the whole dynamics of any point in the square can be described by it's bi-infinite sequence of positions.
Knowing this we can construct any orbit we like and we know it will describe at least one point in the square.
So we can make a periodic point: ...010101.0101010... which alternates from the left to the right. Since we have infinite lengths in both direction, we can make (uncountably) infinitely many of these periodic points.
Or we can make a non-periodic point: ...010001101100000.1010100110111... by, for example, 'counting' in binary as above or just by adding the wrong value to a periodic point i.e. ...01010101.0101011...is non-periodic. There are (uncountably) infinite of these too.
Among this set of non-periodic orbits we can find at least one that comes arbitrarily close to the invariant set. This is trivial since you can take just part of the sequence that describes a point in the invariant set and it would come as close as you like!
I hope you are following since I have just demonstrated that Smale's horseshoe perfectly defines chaos.
Chaotic motion must consist of the following:
- infinitely many periodic orbits
- non-periodic orbits
- dense orbits - ones that come arbitrarily close to any point in the set.
There tends also to be the condition of sensitive dependence on initial conditions but this can be shown through the dense orbits - you can take two sequences that are the same for any arbitrary iterations and in the next they can end up in two different strips i.e. they may start very close but can end up very far apart.
Voila!
Strogatz does give a very basic introduction but for a more detailed approach read the first chapter of "Elements of Applied Bifurcation Theory" by Yuri Kuznetsov. Wiki also has its own explanation.
Monday 21 March 2011
How many drafts...?!
So here we are, nearing the end of my project. Well, actually there are six weeks left til I hand in my thesis but it doesn't feel like it. It feels more like two. :S
I've been asked to do two drafts already. A third one is coming up next week and I'll redo the current one into a fourth. After that they combine into a fifth. Then will follow a sixth from recommended improvements. I'll probably create another couple just for kicks! So that's at leasts one a week...a draft roughly for each month I've worked on it. I'm drowning in them!!
Ah well, at least it means I have shiny pictures for you this week. My draft task this week was to tell the story of one side of my research (decreasing lambda) as purely in images as possible. Obviously the details will be missing but I hope you enjoy the obvious progression and changes in images as lambda varies.
My image report draft is available here.
In other parts of my Masters world I am winding down on lectures and winding up for revision ready for exams in nine weeks. I want to try something new for my revision this year - sort of step it up a level. If anyone has any recommendations that would be very welcome. I have a few ideas but would like to augment these with other influences.
I also have to produce a poster and a website for my Masters project but I'll share them here first to get opinions! I will of course add a link to this blog in my website (cheeky I know!); maybe they'll give me extra marks for initiative and knowledge sharing never mind the pretty pictures!
I've been asked to do two drafts already. A third one is coming up next week and I'll redo the current one into a fourth. After that they combine into a fifth. Then will follow a sixth from recommended improvements. I'll probably create another couple just for kicks! So that's at leasts one a week...a draft roughly for each month I've worked on it. I'm drowning in them!!
Ah well, at least it means I have shiny pictures for you this week. My draft task this week was to tell the story of one side of my research (decreasing lambda) as purely in images as possible. Obviously the details will be missing but I hope you enjoy the obvious progression and changes in images as lambda varies.
My image report draft is available here.
In other parts of my Masters world I am winding down on lectures and winding up for revision ready for exams in nine weeks. I want to try something new for my revision this year - sort of step it up a level. If anyone has any recommendations that would be very welcome. I have a few ideas but would like to augment these with other influences.
I also have to produce a poster and a website for my Masters project but I'll share them here first to get opinions! I will of course add a link to this blog in my website (cheeky I know!); maybe they'll give me extra marks for initiative and knowledge sharing never mind the pretty pictures!
Tuesday 15 March 2011
"To err is human"
And guess what?! I'm human. My error this time was such a small thing but it could have had huge consequences if I had not caught it when I had. Actually it would have been far better to have caught it much much earlier but I had no reason to see problems until this point.
I had successfully combined my manifold examination with the Julia Set calculations into one succinct image for each value of the parameter lambda. Nothing twigged until I sat there showing them to my supervisor and he commented that surely the attractors should actually lie within the prisoner set (the points that remained after the iteration). My manifolds also did not line up with the areas they would be expected to. This meant one of two things. Either I had some scaling issue (quite possible with all the jiggling around I had done to get them on the same image) or something was wrong with either side of the analysis (the MATLAB or DSTool code).
Since the DSTool code had been written by someone far more experienced in the area, it was to my code that I turned my attention to find the problem. Took me a while but (as the error rule says) when I found it it was easy to fix. I like to program quite efficiently and as I was testing the absolute value of Z at each iteration I had set
absZ = abs(Z)*abs(Z);
Now instead of square rooting this after I had tested it I had left it which meant that instead of just dividing by the square of abs(Z) at each iteration, it was dividing by the fourth power of abs(Z). Doh!
Thus all my Julia Set images were actually wrong. Re-running the (easily) corrected code showed just how wrong it had been. But it is fixed now and since then I have been working like stink to analyse the correct progression of Julia Sets.
One of the areas that I have now been progressing into was a direct result of the correction. Once the correct maps were generated, I added a further capability to zoom the section around the interesting circle region. This showed that the points within the Julia Set boundary were actually behaving very much like the stable set patterns seen by the PhD student I have been working with. So I have been expanding my analysis to include calculation of the stable set within the Julia Set boundary. This is likely to contribute to connectedness and other behaviours of the map I have already examined.
As far as I understand it, the stable set is the set of points that go to the attractor(s) via the stable manifold due to the existence of a saddle point. Some points, in the course of being iterated, will end up on the stable manifold or on the saddle itself before slowly reaching the attractor. The stable set is all the points back in time that forward in time end up at the stable manifold (thus more pre-image calculations are involved!).
I have calculated this for a few values and they show promising information - I would have inserted images here but the server is rejecting them...
They should help to determine what the hole actually does to the map at least in the limited sense that I am examining it.
Oh, also I would also have shown you the bifurcation progression through lambda but since the server is rejecting my images I won't be. I'll try next week. Sufficed to say that there is a lot going on. I'm not entirely sure I'll find it easy to stick to the 45 page limit. If anyone has any recommendations for that (things that they would find interesting so think should be included) please let me know. :-)
I had successfully combined my manifold examination with the Julia Set calculations into one succinct image for each value of the parameter lambda. Nothing twigged until I sat there showing them to my supervisor and he commented that surely the attractors should actually lie within the prisoner set (the points that remained after the iteration). My manifolds also did not line up with the areas they would be expected to. This meant one of two things. Either I had some scaling issue (quite possible with all the jiggling around I had done to get them on the same image) or something was wrong with either side of the analysis (the MATLAB or DSTool code).
Since the DSTool code had been written by someone far more experienced in the area, it was to my code that I turned my attention to find the problem. Took me a while but (as the error rule says) when I found it it was easy to fix. I like to program quite efficiently and as I was testing the absolute value of Z at each iteration I had set
absZ = abs(Z)*abs(Z);
Now instead of square rooting this after I had tested it I had left it which meant that instead of just dividing by the square of abs(Z) at each iteration, it was dividing by the fourth power of abs(Z). Doh!
Thus all my Julia Set images were actually wrong. Re-running the (easily) corrected code showed just how wrong it had been. But it is fixed now and since then I have been working like stink to analyse the correct progression of Julia Sets.
One of the areas that I have now been progressing into was a direct result of the correction. Once the correct maps were generated, I added a further capability to zoom the section around the interesting circle region. This showed that the points within the Julia Set boundary were actually behaving very much like the stable set patterns seen by the PhD student I have been working with. So I have been expanding my analysis to include calculation of the stable set within the Julia Set boundary. This is likely to contribute to connectedness and other behaviours of the map I have already examined.
As far as I understand it, the stable set is the set of points that go to the attractor(s) via the stable manifold due to the existence of a saddle point. Some points, in the course of being iterated, will end up on the stable manifold or on the saddle itself before slowly reaching the attractor. The stable set is all the points back in time that forward in time end up at the stable manifold (thus more pre-image calculations are involved!).
I have calculated this for a few values and they show promising information - I would have inserted images here but the server is rejecting them...
They should help to determine what the hole actually does to the map at least in the limited sense that I am examining it.
Oh, also I would also have shown you the bifurcation progression through lambda but since the server is rejecting my images I won't be. I'll try next week. Sufficed to say that there is a lot going on. I'm not entirely sure I'll find it easy to stick to the 45 page limit. If anyone has any recommendations for that (things that they would find interesting so think should be included) please let me know. :-)
Subscribe to:
Posts (Atom)